本文共 4507 字,大约阅读时间需要 15 分钟。

GC之前
说明:该文中的GC算法讲解不仅仅局限于某种具体开发语言。
mutator
mutator 是 Edsger Dijkstra 、 琢磨出来的词,有“改变某物”的意思。说到要改变什么,那就是 GC 对象间的引用关系。不过光这么说可能大家还是不能理解,其实用一句话概括的话,它的实体就是“应用程序”。这样说就容易理解了吧。GC 就是在这个 mutator 内部精神饱满地 工作着。
mutator 实际进行的操作有以下 2 种。
- 生成对象
- 更新指针
mutator 在进行这些操作时,会同时为应用程序的用户进行一些处理(数值计算、浏览网页、 编辑文章等)。随着这些处理的逐步推进,对象间的引用关系也会“改变”。伴随这些变化会 产生垃圾,而负责回收这些垃圾的机制就是 GC。
活动对象 / 非活动对象
我们将分配到内存空间中的对象中那些能通过 mutator 引用的对象称为“活动对象”。反 过来,把分配到堆中那些不能通过程序引用的对象称为“非活动对象”。
根
根(root)这个词的意思是“根基”“根底”。在 GC 的世界里,根是指向对象的指针的“起点” 部分。
这些都是能通过 mutator 直接引用的空间。
评价标准
评价 GC 算法的性能时,我们采用以下 4 个标准。
- 吞吐量
- 最大暂停时间
- 堆使用效率
- 访问的局部性
其他信息(Java语言为例):
1 标记-清除法
优点
①实现简单
说到 GC 标记 - 清除算法的优点,那当然要数算法简单,实现容易了。
另外,如果算法实现简单,那么它与其他算法的组合也就相应地简单。②与保守式 GC 算法兼容
后面介绍的保守式 GC 算法中,对象是不能被移动的。因此保守式 GC 算法跟把 对象从现在的场所复制到其他场所的 GC 复制算法与标记 - 压缩算法不兼容。
而 GC 标记 - 清除算法因为不会移动对象,所以非常适合搭配保守式 GC 算法。事实上,在很多采用保守式 GC 算法的处理程序中也用到了 GC 标记 - 清除算法。
缺点
①碎片化
在 GC 标记 - 清除算法的使用过程中会逐渐产生被细化的分块,不久后就会导致无数的 小分块散布在堆的各处。我们称这种状况为碎片化(fragmentation)。众所周知,Windows 的 文件系统也会产生这种现象。
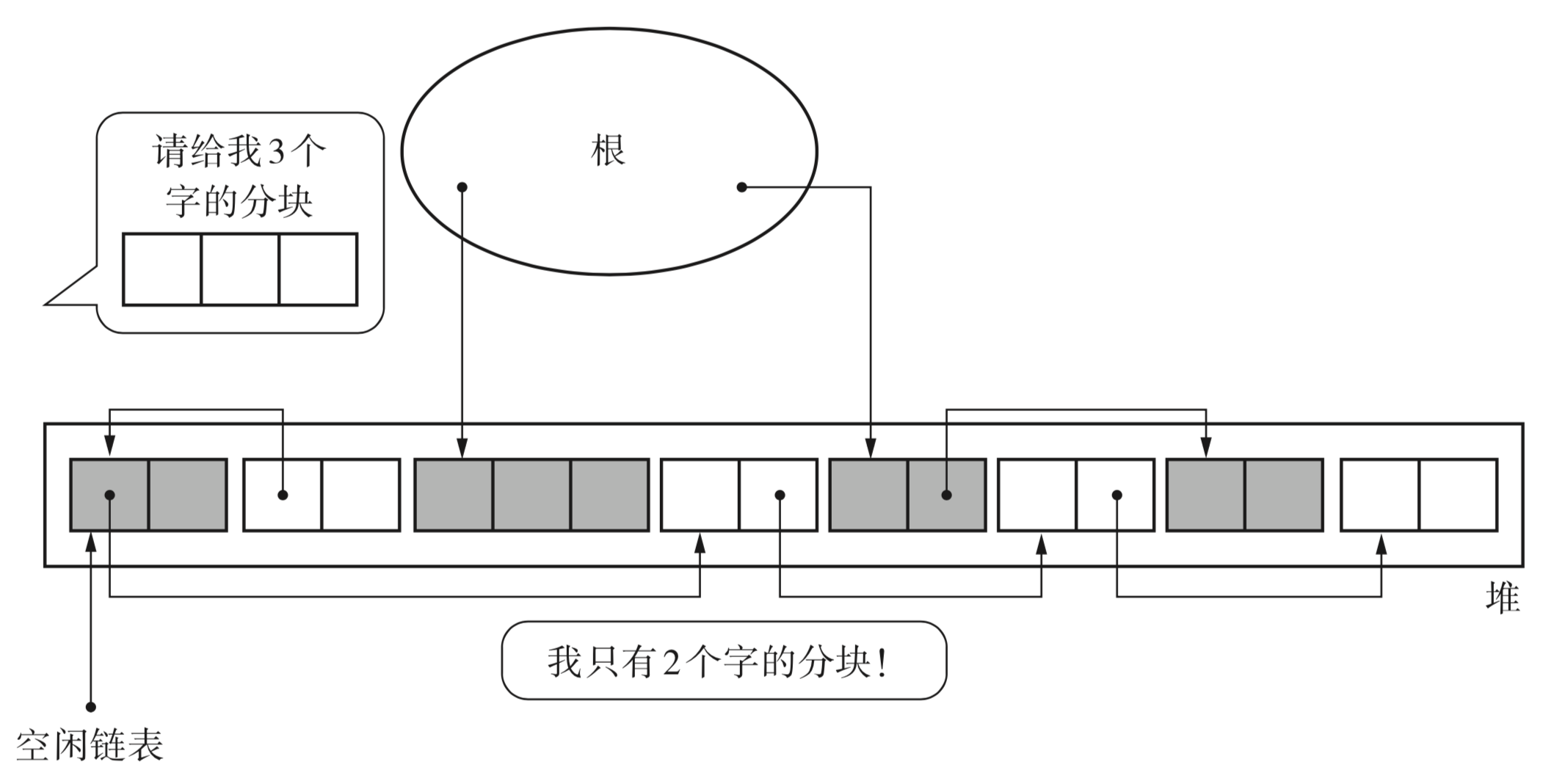
②分配速度
GC 标记 - 清除算法中分块不是连续的,因此每次分配都必须遍历空闲链表,找到足够 大的分块。最糟的情况就是每次进行分配都得把空闲链表遍历到最后。
另一方面,因为在 GC 复制算法和 GC 标记 - 压缩算法中,分块是作为一个连续的内存 空间存在的,所以没必要遍历空闲链表,分配就能非常高速地进行,而且还能在堆允许范围 内分配很大的对象。
③与写时复制技术不兼容
写时复制技术(copy-on-write)是在 Linux 等众多 UNIX 操作系统的虚拟存储中用到的高速化方法。在 Linux 中复制进程,也就是使用 fork() 函数时,大部分内存空间都不会被复制。只是复制进程,就复制了所有内存空间的话也太说不过去了吧。因此,写时复 制技术只是装作已经复制了内存空间,实际上是将内存空间共享了。
在各个进程中访问数据时,能够访问共享内存就没什么问题了。
然而,当我们对共享内存空间进行写入时,不能直接重写共享内存。因为从其他程序访 问时,会发生数据不一致的情况。在重写时,要复制自己私有空间的数据,对这个私有空间 进行重写。复制后只访问这个私有空间,不访问共享内存。像这样,因为这门技术是“在写 入时进行复制”的,所以才被称为写时复制技术。这样的话,GC 标记 - 清除算法就会存在一个问题 — 与写时复制技术不兼容。即使没 重写对象,GC 也会设置所有活动对象的标志位,这样就会频繁发生本不应该发生的复制, 压迫到内存空间。
2 引用计数的算法
优点
①可即刻回收垃圾
在引用计数法中,每个对象始终都知道自己的被引用数(就是计数器的值)。当被引用数 的值为 0 时,对象马上就会把自己作为空闲空间连接到空闲链表。也就是说,各个对象在变成垃圾的同时就会立刻被回收。
另一方面,在其他的 GC 算法中,即使对象变成了垃圾,程序也无法立刻判别。只有当 分块用尽后 GC 开始执行时,才能知道哪个对象是垃圾,哪个对象不是垃圾。也就是说,直 到 GC 执行之前,都会有一部分内存空间被垃圾占用。
②最大暂停时间短
在引用计数法中,只有当通过 mutator 更新指针时程序才会执行垃圾回收。也就是说, 每次通过执行 mutator 生成垃圾时这部分垃圾都会被回收,因而大幅度地削减了 mutator 的最 大暂停时间。
③没有必要沿指针查找
引用计数法和 GC 标记 - 清除算法不一样,没必要由根沿指针查找。减少沿指针查找的次数。
缺点
①计数器值的增减处理繁重
在引用计数法中,每当指针更新时,计数器的值都会随之更新,因此值的增减处理必然会变得繁重。
②计数器需要占用很多位
用于引用计数的计数器最大必须能数完堆中所有对象的引用数。
③实现烦琐复杂
引用计数的算法本身很简单,但事实上实现起来却不容易。如果漏掉了某处,内存管理就无法正确 进行,就会产生 BUG。
④循环引用无法回收
两个对象互相引用,所以各对象的计数器的值都是 1。但是这些对象 组并没有被其他任何对象引用。因此想一并回收这两个对象都不行,只要它们的计数器值都 是 1,就无法回收。
3 GC 复制算法
优点
①优秀的吞吐量
GC 标记 - 清除算法消耗的吞吐量是搜索活动对象(标记阶段)所花费的时间和搜索整体 堆(清除阶段)所花费的时间之和。
另一方面,因为 GC 复制算法只搜索并复制活动对象,所以跟一般的 GC 标记 - 清除算 法相比,它能在较短时间内完成 GC。也就是说,其吞吐量优秀。
尤其是堆越大,差距越明显。GC 标记 - 清除算法在清除阶段所花费的时间会不断增加, 但 GC 复制算法就不会产生这种消耗。毕竟它消耗的时间是与活动对象的数量成比例的。
②可实现高速分配
GC 复制算法不使用空闲链表。这是因为分块是一个连续的内存空间。比起 GC 标记 - 清除算法和引用计数法等使用空闲链表的分配,GC 复制算法明显快得多。
③不会发生碎片化
基于算法性质,活动对象被集中安排在 From 空间的开头对吧。像这 样把对象重新集中,放在堆的一端的行为就叫作压缩。在 GC 复制算法中,每次运行 GC 时 都会执行压缩。
因此 GC 复制算法有个非常优秀的特点,就是不会发生碎片化。也就是说,可以安排分 块允许范围内大小的对象。
④与缓存兼容
在 GC 复制算法中有引用关系的对象会被安排在堆里离彼此较近的位置。这种情况有一个优点,那就是 mutator 执行速度极快。这也是借助压缩来完成的,通过压缩来把有引用关系的对 象安排在堆中较近的位置。
缺点
①堆使用效率低下
GC 复制算法把堆二等分,通常只能利用其中的一半来安排对象。也就是说,只有一半 堆能被使用。相比其他能使用整个堆的 GC 算法而言,可以说这是 GC 复制算法的一个重大的缺陷。
通过搭配使用 GC 复制算法和 GC 标记 - 清除算法可以改善这个缺点。
②不兼容保守式 GC 算法
GC 标记 - 清除算法有着跟保守式 GC 算法相兼容的优点。因 为 GC 标记 - 清除算法不用移动对象。
另一方面,GC 复制算法必须移动对象重写指针,所以有着跟保守式 GC 算法不相容的 性质。
③递归调用函数
在这里介绍的算法中,复制某个对象时要递归复制它的子对象。因此在每次进行复制的 时候都要调用函数,由此带来的额外负担不容忽视。大家都知道比起这种递归算法,迭代算 法更能高速地执行
此外,因为在每次递归调用时都会消耗栈,所以还有栈溢出的可能。
4 GC标记-压缩算法
优点
①可有效利用堆
在 GC 标记 - 压缩算法中会执行压缩,和其他算法相比而言,堆利用效率高。
而且 GC 标记 - 压缩算法不会出现 GC 复制算法那样只能利用半个堆的情况。另一方面,尽管 GC 标记 - 清除算法也能利用整个堆,但因为没有压缩的过程,所以会 产生碎片化,不能充分有效地利用堆。
缺点
①压缩花费计算成本
在 GC 标记 - 清除算法中,清除阶段也要搜索整个堆,不过搜索 1 次就够了。但 GC 标记 - 压缩算法要搜索 3 次,这样就要花费约 3 倍的时间,这是一个相当巨大的缺陷,特别是堆越 大,所消耗的成本也就越大。
4 保守式 GC
什么是保守式 GC
简单来说,保守式 GC(Conservative GC)指的是“不能识别指针和非指针的 GC”。
优点
①语言处理程序不依赖于 GC
保守式 GC 的优点在于容易编写语言处理程序。处理程序基本上不用在意 GC 就可以编 写代码。语言处理程序的实现者即使没有意识到 GC 的存在,程序也会自己回收垃圾。因此 语言处理程序的实现要比准确式 GC 简单。
缺点
①识别指针和非指针需要付出成本
②错误识别指针会压迫堆
当存在貌似指针的非指针时,保守式 GC 会把被引用的对象错误识别为活动对象。如果 这个对象存在大量的子对象,那么它们一律都会被看成活动对象。因为程序把已经死了的非 活动对象看成了活动对象,所以垃圾对象会严重压迫堆。
③能够使用的 GC 算法有限
5 分代垃圾回收
优点
①吞吐量得到改善
通过使用分代垃圾回收,可以改善 GC 所花费的时间(吞吐量)。正如 Ungar 所说的那样:“据实验表明,分代垃圾回收花费的时间是 GC 复制算法的 1/4。”可见分代垃圾 回收的导入非常明显地改善了吞吐量。
另一方面,因为老年代 GC 很费时间,所以我们没法缩短 mutator 的最大暂停时间。关 于使用分代垃圾回收来缩减 mutator 最大暂停时间的方法
缺点
①在部分程序中会起到反作用
对对象会活得很久的程序执行分代垃圾回收,就会产生以下两个问题。
- 新生代GC所花费的时间增多
- 老年代GC频繁运行
考虑到这两点,恐怕我们没法利用到分代垃圾回收的优点,或者就算利用到了,效果也 甚微。
6 增量式垃圾回收
优点
①缩短最大暂停时间
增量式垃圾回收不是一口气运行 GC,而是和 mutator 交替运行的,因此不会长时间妨碍 到 mutator 的运行。
增量式垃圾回收适合那些比起提高吞吐量,更重视缩短最大暂停时间的应用程序。
②降低了吞吐量
想要优先提高吞吐量,最大暂停时间就会增加;想要优先缩短最大暂停时间, 吞吐量就会恶化。这两者是一个权衡关系。至于要优先哪一方,则要根据应用程序而定。
参考文献:《垃圾回收的算法与实现》
欢迎关注 与 收藏文章 !
欢迎关注 !个人介绍:
高广超:多年一线互联网研发与架构设计经验,擅长设计与落地高可用、高性能、可扩展的互联网架构。
本文首发在 转载请注明!

